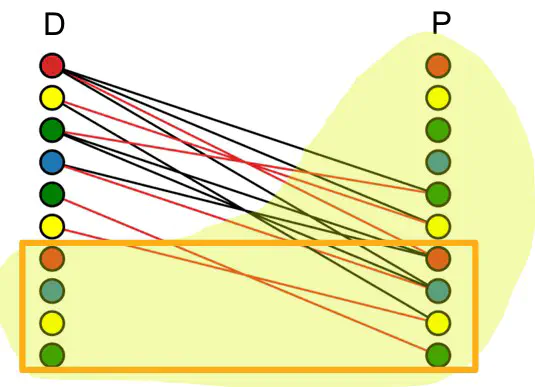
A taxi routing problem can be solved via bipartite matching, where a maximum cardinality matching corresponds to the minimum number of taxis needed to cover all trips. We prove a min-max theorem: the maximum number of pairwise incompatible trips equals the minimum number of taxis needed. We also demonstrate the proble, on an NYC taxi dataset and obtain a 35% reduction in the total number of taxis needed. Part of the work is integrated into a lab of ENGRI 1101: Engineering Applications of OR.